
Rompecabezas numéricos para tu cerebro

Rompecabezas numéricos para tu cerebro
En esta guía ofrecemos una gama de consejos prácticos sobre cómo resolver rompecabezas Kakuro, con dificultades que van desde el nivel principiante hasta el nivel experto.
Para resumir las reglas: Kakuro es un juego de rompecabezas en un tablero como crucigramas donde se utilizan dígitos para hacer que suman los valores especificados en los cuadrados de definición del tablero. Además, dentro de cada grupo de suma, cada dígito puede aparecer una vez como máximo.
La forma tradicional de resolver un rompecabezas Kakuro es incremental: mediante el uso de la información existente en el tablero, usted puede encontrar con certeza el valor de una celda específica que puede tomar sólo un valor posible. Entonces ese valor se rellena y el proceso se repite hasta que se descubran todas las celdas del tablero.
En algunas situaciones, no hay ninguna célula de placa específica que tenga una sola posibilidad. En esos casos, cada una de las posibilidades debe explorarse por sí sola y eliminarse mediante contradicciones hasta que sólo quede un curso de acción.
Fueron presentando a continuación varios métodos para hacer progresos en la resolución del rompecabezas real.
Hay algunas definiciones que se pueden resolver solo de una manera específica:
y así sucesivamente... Por lo general, puede pasar el cursor sobre una cuadrícula de Kakuro sobre el número de definición y aparecerá una descripción emergente que contiene todas las posibilidades de escribir esa suma con dígitos únicos en el número de celdas disponibles.
Las sumas que se pueden escribir de una manera única suelen ser sumas bajas o altas que fuerzan dígitos bajos/altos en la respuesta para alcanzarlos.
Tener una forma única de escribir la suma ayuda, pero tenga en cuenta que todas las permutaciones son válidas y aún necesita averiguar qué permutación real usar en el tablero.
 |
 |
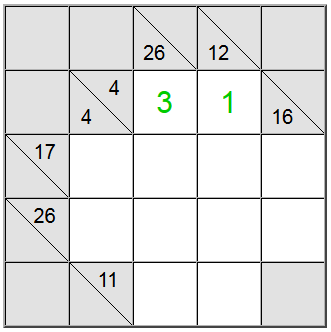 |
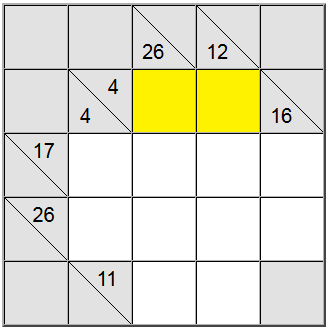
Para las celdas amarillas resaltadas arriba, sólo hay una forma de escribir la suma: 4 = 1 + 3. Sin embargo, todavía tenemos que averiguar qué permutación (1 + 3 o 3 + 1) usar.
Resulta que la definición vertical 26 nos ayuda: una suma en 4 celdas que contendría el dígito 1 sería como máximo 1 + 9 + 8 + 7 = 25. Dado que nuestra suma es 26, resulta que el dígito 1 no puede ser parte de la suma. Por lo tanto, el único orden restante para los cuadrados amarillos es 3 + 1.
 |
 |
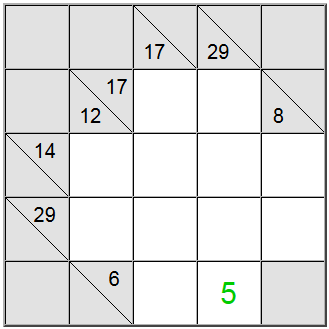 |
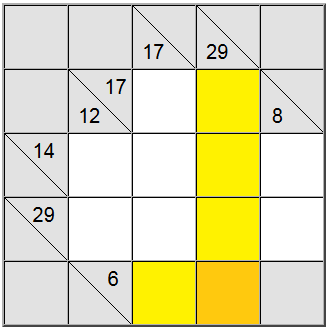
En el tablero anterior, los cuadrados amarillos horizontales se pueden escribir como 6 = 1 + 5 o 6 = 2 + 4. La suma amarilla vertical sólo se puede escribir como 29 = 5 + 7 + 8 + 9.
El cuadrado amarillo encontrado en la intersección de esas dos definiciones de suma debe contener el mismo dígito, por lo que debe haber un dígito común presente en las definiciones horizontal y vertical para poder compartirlo entre ellas. Mirando las posibilidades anteriores podemos descubrir fácilmente que 5 es el único dígito que respeta este criterio.
Esta técnica funciona especialmente bien cuando se cruza una suma baja con una definición de suma alta. Las definiciones de suma baja y suma alta son las que tienen un número de definición de suma baja o alta (6 y 29 respectivamente para nuestro ejemplo) en comparación con el número de celdas disponibles. Debido a que 6 es relativamente bajo, forzará dígitos bajos en la representación de suma, y 29 forzará los dígitos altos (con el fin de alcanzar estas sumas usando el número dado de celdas). Por lo tanto, es probable que la intersección de dígitos bajos y altos contenga sólo un candidato para el valor de celda real.
 |
 |
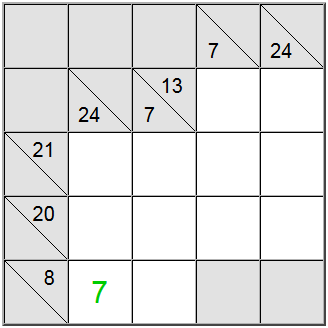 |
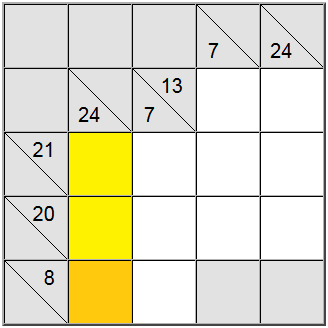
A veces es útil calcular el valor máximo o mínimo para un grupo de suma. Esto puede darle una idea de cuál es el rango válido de dígitos para esa suma en particular, lo que a su vez le ayudará a hacer correlación con otras restricciones y averiguar las asignaciones únicas en el tablero.
En el ejemplo anterior, las celdas verticales amarillas solo aceptan valores iguales a 7 o superiores. Si intenta asignar un 6, puede averiguar fácilmente que 6 + 9 + 8 = 23 para que la suma de definición de 24 no sea alcanzable.
Debido a que 7 es un mínimo, la definición horizontal que tiene 8 como suma fuerza el 7 en esa posición.
Practicar es la mejor manera de ver cómo se puede aplicar este consejo en juegos reales de Kakuro. Juega un rompecabezas de verdad. Le deseamos buena suerte y mucha diversión!
© 2026 - Todos los derechos reservados - Página de contacto - Política de privacidad - DE | EN | ES | FR | IT | JA | LT | LV | NL | PL | PT | RO | SV | TR